Invariants by derivation property for vectors
Given a vector field $A=\partial x+u_1 \partial u+\cdots+\phi\partial u_{m-1}$ encoding an $m$-th order ODE, and $X$ a vector field such that
$$ [X,A]=\lambda X+\mu A $$(that is, a generalized Cinf-symmetry ODE). Then if $w$ and $y$ are differential invariants of $X$ then $\dfrac{A(w)}{A(y)}$ is also a differential invariant.
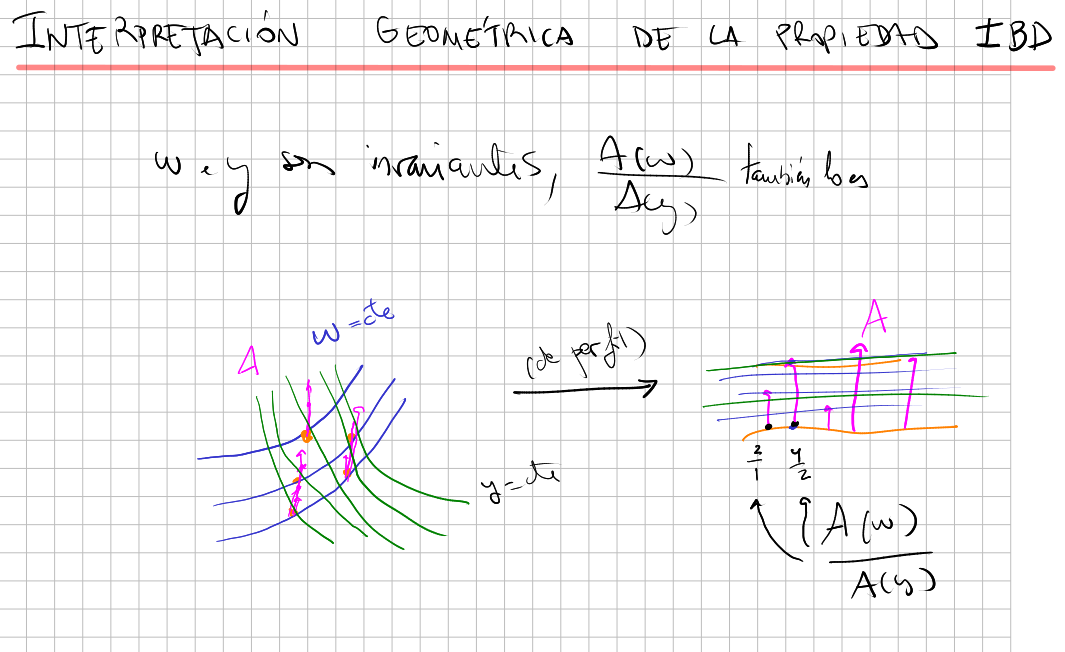
IBD property is also applied to distributions.
It turns out that the vector fields above are the more general class of vector fields satisfying the IBDP (@MR2001541). But, are they independent?
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: